



This is kind of a newer interest to me. I am fairly good with GPS navigation and how it works, but I wanted to get a better understanding of how basic navigation is done on paper with the basic math required. I'll guess I'll learn as I go and post it as I learn it.
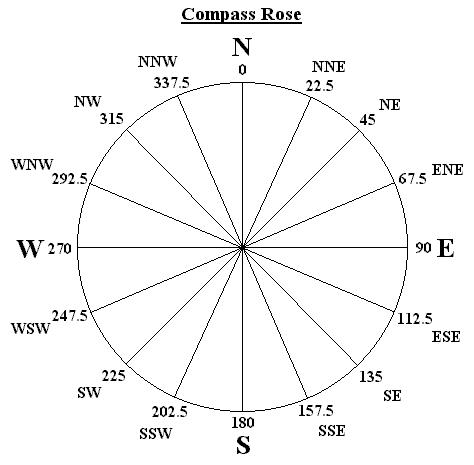
Here is a simple compass rose diagram. It shows the compass points as well as the more well known degree headings.
Longitude and Latitude is measured in Degrees, Minutes and Seconds. It can be aligned North and West or South and East, this depends on what hemisphere you live in. If you live in the Northern Hemisphere then Lon/Lat is measured North and West. If you live in the Southern Hemisphere then Lon/Lat is measured South and East. Below is the format.
| ddmm.ss N dddmm.ss W | or | 3917.78 N 07923.84 W |

This is the stuff I'm trying to learn/figure out onmy own. This diagram is showing finding the distance between to points on a sphere. Which is basically what is required to find the distance between two points on the face of the earth. Below is also math for this process. It's basically geometric math (I failed geometry in school). But I think I can get this stuff.
First, in order to find the distance, the Lat/Lon data must be in a useable form. In this case it needs to be in decimal form. This can be done by applying a simple formula to the Latitude and Longitude. The latitude in the nothern hemisphere must be expressed as a negative value. In the southern hemispere, the longitude would be expressed as a negative.
I will use to points to show how this works.
There are two more values that we need to calculate the distance. One is Longitude of point one subtracted from the Longitude of point two. Two, we need the Latitude of point one subtracted from the latitude of point two.
OK, now we need to give these values some varible names.
After going through all of this math, you should be able to come up with the proper distance calculation. D = Total Distance = -156.9147878. This is the value in miles. Since the US is in the northern hemisphere, you can just drop the (-) and you get the distance 156.915 miles.
So far I have had VERY mixed results with this. Some are close and some are VERY far off. If anyone does try these, I would be curious to how well it works out for them. There is one other formula I came across and it has also had mixed results.


